Does the proof of the Riemann hypothesis really bring the whole of ecommerce to its knees ?

Recently, The Guardian published an announcement titled "Maths holy grail could bring disaster for internet". This announcement was then declined in several variants over the internet (1, 2), commenting a new discovery that could "bring the whole of ecommerce to its knees, overnight".
So, companies whose business depends on cryptography started contacting us, worried by the implications of this cryptographic breakthrough.

This note attempts to answer that question, in a way most can understand. Parts of the discussion are probably oversimplified, but people noticing these shortcuts are able to make an opinion by themselves (I am of course open to any suggestion that would improve this note).

What is it all about?

The underlying event is that a mathematician named Louis de Branges claims to have proved the Riemann hypothesis. This hypothesis, first formulated by Bernhard Riemann in 1859, is a conjecture about the distribution of the zeros of Riemann's zeta function. What is relevant for cryptologists is that the Riemann Hypothesis (RH) has been proved equivalent to a relationship describing the distribution of prime numbers among integers (in fact, a strengthening of the well-known prime number theorem; see below links for more details). So, there is a relationship between RH and a possible structure in the distribution of primes, and primes are widely used in cryptography.

What are primes used for?

Prime numbers are very common in public-key cryptography. For example, the well-known RSA algorithm involves taking two big primes at random and disclosing their product. If someone can recover the two primes from the product, then he can also decrypt all the messages protected by that key.

What would be the impact of a structure among primes?

In fact, we need some structure in primes' distribution. The classical methods to generate secret primes (i.e. pick a random odd number and check if it is prime; if it is not, pick another one - or add two to it - and check again) rely on the fact that primes are "evenly" distributed among integers to ensure that we will not have to wait forever (with some safeguards deployed in the - always possible - case we fall in a bad zone).

The disastrous case would be a result showing a "too tight" structure among primes. Such a characterization could for example be used to develop shortcuts in factorization methods, which could drastically increase the size of numbers that can be factored.

So, what is the impact of de Branges' result?

Let us first note that the proof has not been submitted to peer review yet, and therefore might still be erroneous (de Branges had previously produced proofs of the Riemann hypothesis, which later turned out to be wrong). But - although some announcements present possible wrongness as the last hope for cryptography - this is probably not the most important point here.

In fact, de Branges' result comes rather to confirm something we believed to be true than to highlight a revolutionary and unexpected fact about primes. RH's characterization of primes' distribution states that, as x goes to infinity, the number of primes smaller than x tends to

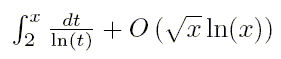
The first term gives the general distribution, and the second describes an error-margin, corresponding to some random pattern in primes' exact locations. Without it, we could tell exactly where primes are by computing the difference of that function's value between two bounds. This error term is large enough to leave plenty of uncertainty about primes' locations, so this structure is not sufficiently tight, in the above sense.

The result itself, "Riemann's hypothesis has been proved true", does not have a very deep impact on cryptography. If people were just waiting for that information to be able to develop efficient factorization algorithms, for example, they could very well just have assumed that the hypothesis was true - this is what most mathematicians believe, anyway - and started writing. Even a result that is proven on the assumption that RH is true is taken very seriously by the scientific community. As a matter of fact, factorization algorithms based on the assumption that RH (or generalizations of it) is true already exist.

Now, this does not mean that de Branges' work would be uninteresting. Besides the result, the proof itself could describe a more precise structure in the distribution of zeroes of the zeta function, or could provide some insights opening further research directions. The press releases I have read, however, do not seem to refer to that.

Finally, it is worth noting that Riemann's hypothesis is asymptotic, and thus by definition is only proved to apply for huge values, with huge meaning "bigger than what you thought". de Branges' results might also apply for "human-scale" values… or not.

So, the bottom line of all this is "this result (if true) might open new research areas, which could in turn lead to improvements requiring a drastic revision of our vision of public-key cryptography". Yes, and maybe one of the thousands other researchers in number fields will suddenly come up with a breakthrough in factorization methods - we know that, and live with it. In the current situation, it is not clear whether the first event is more likely than the second.

About Riemann's zeta function
http://www.math.ubc.ca/~pugh/RiemannZeta/RiemannZetaLong.html

About the connection between zeta function and prime numbers
http://en.wikipedia.org/wiki/Riemann_hypothesis